Skip to main content

Turunan Fungsi

Pertambahan suatu variabel 𝑥 dilambangkan dengan ∆𝑥 adalah perubahan dalam 𝑥  bila 𝑥  membesar atau mengecil dari suatu nilai awal 𝑥 = 𝑥₀ menjadi nilai berikutnya 𝑥 = 𝑥₁ pada jangkauannya, dalam hal ini ∆𝑥 = 𝑥₁ - 𝑥₀. 


Bila variabel 𝑥 diberi pertambahan sebesar ∆𝑥, maka suatu fungsi y = f(𝑥) juga akan menerima perubahan dalam y sebesar 

perubahan dalam y

Hasil bagi 

laju perubahan rata-rata fungsi pada selang x=x0 dan x=x1=x0+∆x


disebut laju perubahan rata-rata fungsi pada selang 𝑥 = 𝑥₀ dan 𝑥 = 𝑥₁= 𝑥₀ + ∆𝑥. 

Turunan 

Turunan atau derivative suatu fungsi y = f(𝑥) di titik 𝑥 = 𝑥₀ adalah limit laju perubahan rata-rata fungsi saat ∆𝑥 mendekati nol tetapi tidak nol dan didefinisikan sebagai 

Turunan atau derivative suatu fungsi y = f(𝑥) di titik 𝑥 = 𝑥₀


Asalkan limitnya ada. 



Contoh 1. Cari turunan y = f(𝑥) = 𝑥² +1 pada 𝑥 = 𝑥₀. Hitung nilai turunan pada 
a) 𝑥₀ = 2, 
b) 𝑥₀ = 3. 

Jawab: 



a) di 𝑥₀ = 2 nilai turunan adalah 2.2 = 4. 
b) di 𝑥₀ = 3 nilai turunan adalah 2.3 = 6 

Dalam mencari turunan suatu fungsi, indeks 0 biasanya dihilangkan dan turunan y = f(𝑥) terhadap 𝑥 dituliskan dengan

turunan y = f(𝑥) terhadap 𝑥


Beberapa notasi lain yang sering digunakan untuk turunan antara lain 

notasi lain yang sering digunakan untuk turunan


Contoh 2. Cari dy/d𝑥 jika y = 𝑥³ + 𝑥² -5. Berapa nilai dy/d𝑥 di 𝑥 = 4, 𝑥= 0, dan 𝑥 = -1 ?

Jawab:

Cari dy/d𝑥 jika y = 𝑥³ + 𝑥² -5

Notasi untuk dy/d𝑥 di 𝑥 = a bisa ditulis sebagai 

Notasi untuk dy/d𝑥 di 𝑥 = a


jadi 
dy/d𝑥 di 𝑥 = 4, 𝑥= 0, dan 𝑥 = -1

Contoh 3. Cari y’ jika y = (𝑥-1)/(𝑥+1). Berapa nilai  y’ di 𝑥 = 0, 𝑥 = 1, dan 𝑥 = -1 ?

Jawab:

Cari y’ jika y = (𝑥-1)/(𝑥+1)

y’ di 𝑥 = 0 adalah y′(0)=2(0+1)2=2
y’ di 𝑥 = 1 adalah y′(1)=2(1+1)2=12 
y’ di 𝑥 = -1 tidak ada



Labels

Labels:

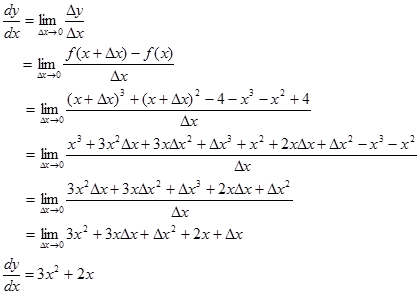
Comments

Post a Comment

Popular posts from this blog

Contoh Soal integral parsial kuliah

  Jika $u$ dan $v$ adalah fungsi $x$ yang dapat dideferensiasi, maka Untuk dapat menggunakan rumus integral parsial (sebagian), integral yang diberikan harus dipisahkan menjadi dua bagian, satu bagian adalah $u$ dan bagian lainnya yang memuat $dx$ adalah $dv$. Aturan umum integral parsial adalah sbb: a) Bagian yang dipilih sebagai $dv$ harus dapat segera diintegralkan. b) $∫vdu$  harus lebih mudah dari $∫udv$ Contoh-1 . cari $\int{x^{3}e^{x^{2}}}dx$ Ambil $u=x^2$-->$du=2xdx$,  dan $dv=xe^{x^{2}}dx$-->$v=\int{xe^{x^{2}}}dx=\frac{1}{2}e^{x^{2}}$ dengan aturan  integral parsial   maka   Cara lain   Contoh-2 . cari $\int_{0}^{5}{x\ln(x+4)}dx$ Ambil $u=\ln(x+4)$-->$du=\frac{dx}{x+4}$,  dan $dv=xdx$-->$v=\int{xdx=\frac{1}{2}x^2}$ dengan aturan  integral parsial maka Integral tentu yang ditanyakan adalah: Rumus-rumus Reduksi  Integral Parsial Langkah-langkah yang rumit dalam penyelesaian integral parsial dapat dikurang...
Post a Comment
Read more

Turunan Fungsi Implisit

Suatu persamaan $f(x,y)=0$ pada jangkauan terbatas dari variabel-variabel tertentu dikatakan mendefinisikan $y$ sebagai fungsi $x$ secara implisit.    Contoh 1:  a) Persamaan $xy+x-y-2=0$, dengan $x≠1$ mendefinisikan fungsi $y=\frac{(2-x)}{(x-1)}$.  b) Persamaan $x^{2}+y^{2}-16=0$, mendefinisikan fungsi $y=\sqrt{16-x^{2}}$  jika $|x|≤4$ dan $y≥0$, dan fungsi  $y=-\sqrt{16-x^{2}}$  jika $|x|≤4$ dan $y≤0$. Perhatikan, lingkarannya harus dianggap terdiri dari dua busur yang bertemu di $(-4,0)$ dan $(4,0)$.   Untuk mendapatkan turunan fungsi implisit caranya turunkan kedua ruas terhadap $x$.    Contoh 2 . Cari $y’$ dan $y’’$ pada contoh 1.a. Berapa $y’$ di $x=2$ dan $y’’$ di $x=3$?  Solusi:  Mencari $y’$ Mencari $y’’$   Contoh 3 .  Cari $y’$ dan $y’’$ pada contoh 1.b. Berapa $y’$ di $x=3$ dan $y’’$ di $x=3$?  Iklan. semoga Anda tertarik Solusi:  Mencari $y’$    Mencari $y’...
Post a Comment
Read more

Turunan Fungsi Aljabar

Fungsi aljabar adalah fungsi yang paling sering ditemui dalam permasalahan matematika yang meliputi fungsi rasional, linear, kuadrat, kubik dan seterusnya. Suatu fungsi aljabar (bidang) adalah fungsi yang persamaannya dapat ditulis sebagai Dengan $u_{n}(x)$ adalah suatu polinomial dalam $x$. Contoh. fungsi kuadrat $y = x^{2} – 10x+25$. Dari fungsi ini maka didapat $n=2, a=0, b=0, c=1, d=-1, e=10, f=-25$, dan $u_{3}(x)=u_{4}(x)=…=u_{n}(x)=0$. Turunan fungsi aljabar  dapat diperoleh dengan menerapkan definisi turunan fungsi pada fungsi-fungsi aljabar. Suatu fungsi aljabar (begitu juga fungsi transenden misalnya fungsi trigonometri) dapat diturunkan di $x = a $ jika fungsi itu mempunyai turunan di titik tersebut. Suatu fungsi aljabar dapat diturunkan pada suatu selang  jika fungsi itu mempunyai turunan di setiap titik pada selang tersebut. 1. Turunan fungsi konstan Misalkan $y =f(x) = c$, dengan $c$ sebuah konstanta sembarang maka Bukti Contoh 2...
Post a Comment
Read more