Integral Substitusi dan Substitusi Efektif

Teknik integral substitusi efektif adalah teknik pengintegralan dengan mengubah bentuk fungsi integran yang tidak lazim menjadi bentuk integran yang umum yaitu bentuk-bentuk yang ada dalam rumus-rumus dasar integral.

Substitusi ini tidak memiliki aturan khusus namun sering dapat ditebak dari bentuk fungsi integrannya mengacu pada rumus-rumus dasar integrasi. Umumnya, substitusi ini berbentuk integral substitusi aljabar.

Banyak langkah substitusi bisa beragam mulai dari satu kali, dua kali, tiga kali, dan mungkin bisa lebih dari itu. Atas dasar itu, substitusi efektif tidak dapat diartikan sebagai substitusi yang sekaligus mengubah fungsi integran menjadi lebih mudah, namun ketepatan dalam menukar variabel.

1. Substitusi Satu kali

Berikut adalah contoh-contoh substitusi satu kali.

Contoh-1. cari $\int{3x\sin(x^2)dx}$

Ambil $x^2=u$-->$2xdx=du$-->$xdx=\frac{du}{2}$

Contoh-2. cari $\int{6x^2\sqrt{4-x^3}dx}$

Ambil $4-x^3=u$-->$-3x^2dx=du$-->$x^2dx=-\frac{du}{3}$

Contoh-3. cari $\int{x^5\sqrt{5+x^3}dx}$

Ambil $5+x^3=u^2$-->$x^3=u^2-5$-->$3x^2dx=2udu$

2. Substitusi Dua kali

Berikut adalah contoh substitusi dua kali.

Contoh-4. cari $\int{\frac{\sqrt{5x+x^2}dx}{x^4}}$

Ambil $x=1/u$-->$dx=-u^{-2}du$

Ambil $5u+1=v^2$-->$du=\frac{2vdv}{5}$

3. Substitusi Tiga kali

Berikut adalah contoh substitusi tiga kali.

Contoh-5. cari $\int{\frac{\sqrt{-9+16x-x^2}dx}{3(x-1)^4}}$

Ambil $x-1=u$-->$dx=du$

Ambil $u=\frac{1}{v}$-->$du=-\frac{dv}{v^2}$

Ambil $2v-7=w^2$-->$dv=wdw$

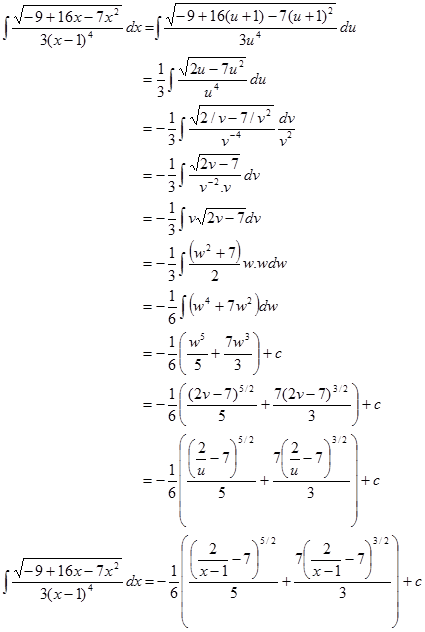Comments

Metode Penyelesaian Limit

A. Limit fungsi f(x) untuk x menuju nilai tertentu (x→a,a∈R) 1. Substitusi langsung pada fungsinya Misalkan ingin diketahui hasil limit f(x) saat x mendekati c. Jika f(c) tidak tak terdefinisi atau tidak tak tentu atau tidak tak hingga, maka umumnya nilai limit f(x) saat x mendekati c adalah f(c). Cara ini diperoleh dengan memanfaatkan kekontinyuan fungsi di titik c. Contoh a) b) Jika fungsi tidak kontinyu di c maka cara ini tidak bisa digunakan. Contoh a) tidak bisa substitusi langsung karena untuk x=1 fungsi memuat bentuk tak tentu 0/0. b) Diberikan Tentukan Jawab: Dari fungsi jelas f(4)=0 tetapi . Jadi tidak berlaku walaupun f(4) ada yaitu 0 ini tidak bisa memakai cara substitusi langsung. 2. Menyederhanakan bentuk rasional Cara ini diperoleh dengan membagi faktor yang sama pada pembilang dan penyebut. Contoh a) b) 3. Modifikasi bentuk k/0 dengan k ≠ 0. Contoh Bentuk ini memuat 2/0...

Contoh Soal integral parsial kuliah

Jika $u$ dan $v$ adalah fungsi $x$ yang dapat dideferensiasi, maka Untuk dapat menggunakan rumus integral parsial (sebagian), integral yang diberikan harus dipisahkan menjadi dua bagian, satu bagian adalah $u$ dan bagian lainnya yang memuat $dx$ adalah $dv$. Aturan umum integral parsial adalah sbb: a) Bagian yang dipilih sebagai $dv$ harus dapat segera diintegralkan. b) $∫vdu$ harus lebih mudah dari $∫udv$ Contoh-1 . cari $\int{x^{3}e^{x^{2}}}dx$ Ambil $u=x^2$-->$du=2xdx$, dan $dv=xe^{x^{2}}dx$-->$v=\int{xe^{x^{2}}}dx=\frac{1}{2}e^{x^{2}}$ dengan aturan integral parsial maka Cara lain Contoh-2 . cari $\int_{0}^{5}{x\ln(x+4)}dx$ Ambil $u=\ln(x+4)$-->$du=\frac{dx}{x+4}$, dan $dv=xdx$-->$v=\int{xdx=\frac{1}{2}x^2}$ dengan aturan integral parsial maka Integral tentu yang ditanyakan adalah: Rumus-rumus Reduksi Integral Parsial Langkah-langkah yang rumit dalam penyelesaian integral parsial dapat dikurang...

Turunan Fungsi Implisit

Suatu persamaan $f(x,y)=0$ pada jangkauan terbatas dari variabel-variabel tertentu dikatakan mendefinisikan $y$ sebagai fungsi $x$ secara implisit. Contoh 1: a) Persamaan $xy+x-y-2=0$, dengan $x≠1$ mendefinisikan fungsi $y=\frac{(2-x)}{(x-1)}$. b) Persamaan $x^{2}+y^{2}-16=0$, mendefinisikan fungsi $y=\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≥0$, dan fungsi $y=-\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≤0$. Perhatikan, lingkarannya harus dianggap terdiri dari dua busur yang bertemu di $(-4,0)$ dan $(4,0)$. Untuk mendapatkan turunan fungsi implisit caranya turunkan kedua ruas terhadap $x$. Contoh 2 . Cari $y’$ dan $y’’$ pada contoh 1.a. Berapa $y’$ di $x=2$ dan $y’’$ di $x=3$? Solusi: Mencari $y’$ Mencari $y’’$ Contoh 3 . Cari $y’$ dan $y’’$ pada contoh 1.b. Berapa $y’$ di $x=3$ dan $y’’$ di $x=3$? Iklan. semoga Anda tertarik Solusi: Mencari $y’$ Mencari $y’...

Kuliah Matematika

Search This Blog